Lekcja zawiera 4-godzinne video, a w nim 10 rozwiązanych zadań zamkniętych, 5 zadań kodowanych i 15 otwartych, dotyczących planimetrii, czyli geometrii na płaszczyźnie, na poziomie rozszerzonym szkoły średniej. Jest ona pierwszą z trzech lekcji tej części Kursu, dotyczących geometrii.
Obejmuje takie zagadnienia jak: kąty, trójkąty, czworokąty, trapez, romb, równoległobok, figury podobne, pole, obwód, okrąg wpisany i opisany na trójkącie oraz czworokącie, twierdzenie Pitagorasa, twierdzenie sinusów, twierdzenie cosinusów – te dwa ostatnie to klasyk na rozszerzeniu.
Lekcja ta wymaga nieco wyobraźni i ciekawych pomysłów na rozwiązanie. Często warto zastosować pewne triki, by dojść do ostatecznego wyniku. Spokojnie, wszystko to postaram się Ci pokazać, byś przede wszystkim zrozumiał ich działanie. 🙂
Oprócz ogromnej ilości wzorów zawartych w tablicach maturalnych, przedstawiam tu wiele przydatnych i cennych twierdzeń, schematów i własności. Przydadzą się nawet te poznane jeszcze w podstawówce.
Spis treści:
- Zadanie 1: twierdzenie cosinusów, określenie kątów trójkąta o podanych bokach [05:48]
- Zadanie 2: pole trójkąta, a długości boków [14:32]
- Zadanie 3: czworokąt, połączenie środków boków [21:00]
- Zadanie 4: twierdzenie o dwusiecznej [29:16]
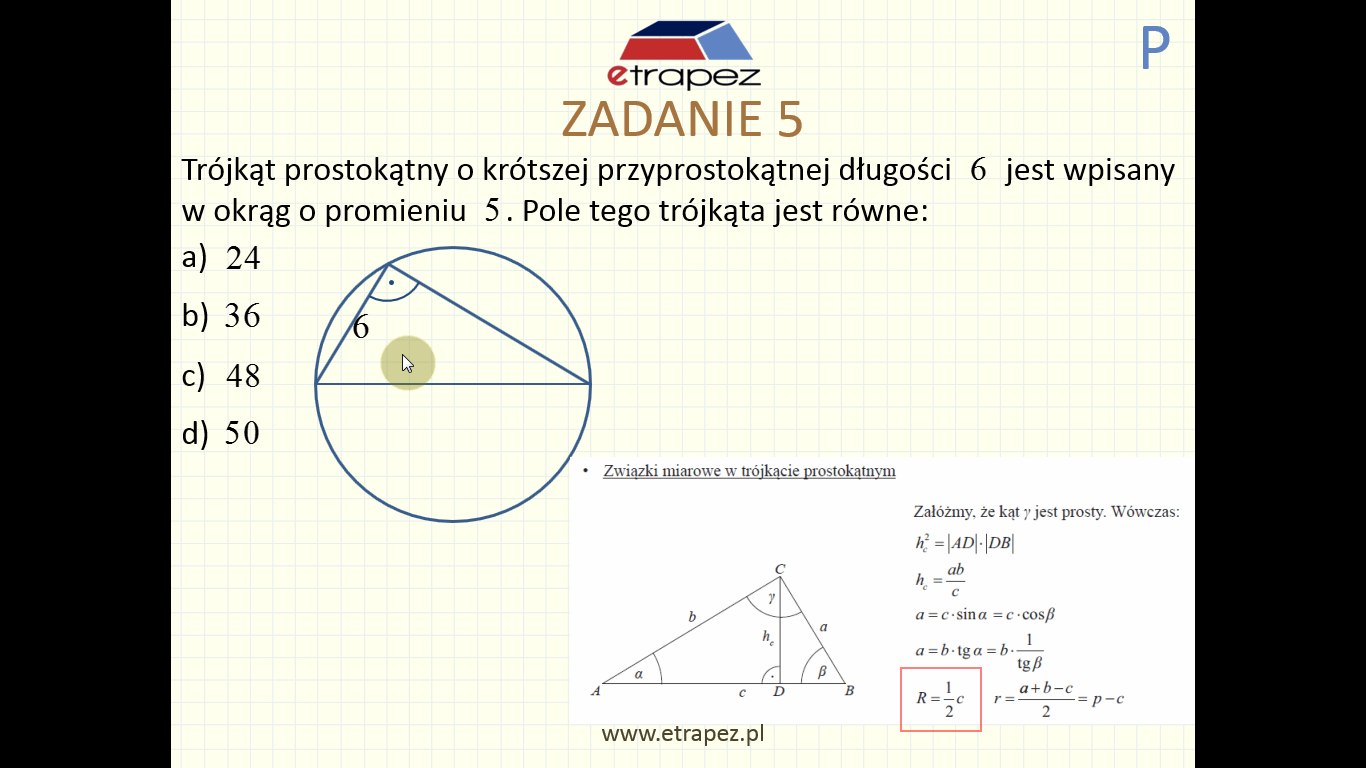
- Zadanie 5: długość środkowej w trójkącie, trójkąt prostokątny [32:30]
- Zadanie 6: okrąg, cięciwa, sieczna, twierdzenie o odcinkach siecznej i stycznej [35:25]
- Zadanie 7: trapez, przekątna dzieli go na dwa trójkąty podobne, obliczenie długość dłuższej podstawy [44:30]
- Zadanie 8: półokrąg wpisany w trójkąt prostokątny [50:48]
- Zadanie 9: okrąg wpisany w trapez prostokątny, długość dłuższego ramienia [56:52]
- Zadanie 10: czworokąt z podanymi kątami, okrąg opisany i wpisany w czworokąt [1:01:28]
- Zadanie 11: trójkąt, podane boki, obliczenie promienia okręgu opisanego na tym trójkącie, wykorzystanie wzoru Herona na pole trójkąta [1:07:04]
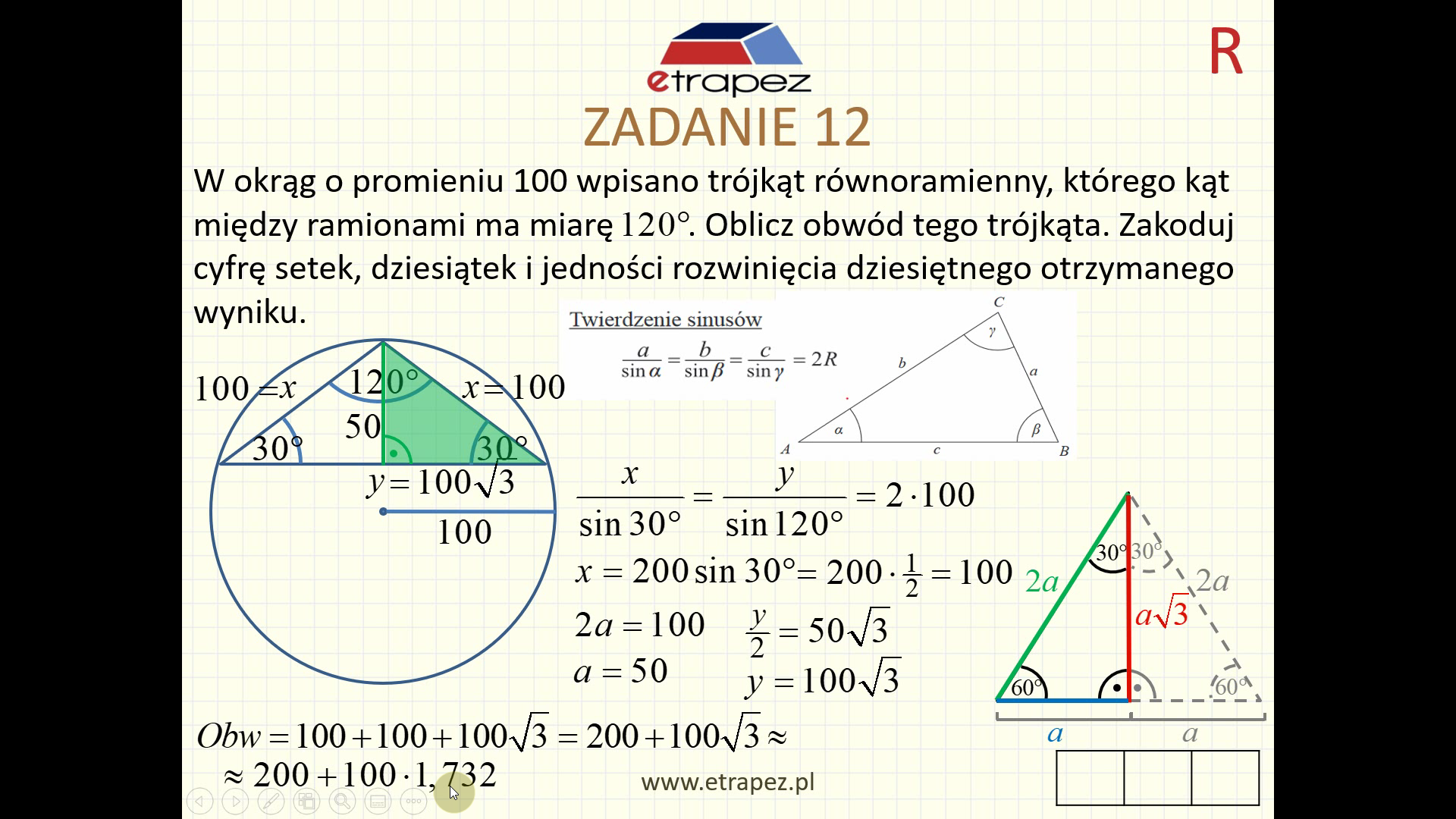
- Zadanie 12: okrąg opisany na trójkącie rozwartokątnym, twierdzenie sinusów [1:13:08]
- Zadanie 13: trapez, podane boki, tangens najmniejszego konta, twierdzenie Talesa [1:21:37]
- Zadanie 14: trójkąt prostokątny, poprowadzone środkowe z kątów ostrych, pole trójkąta ABM [1:29:02]
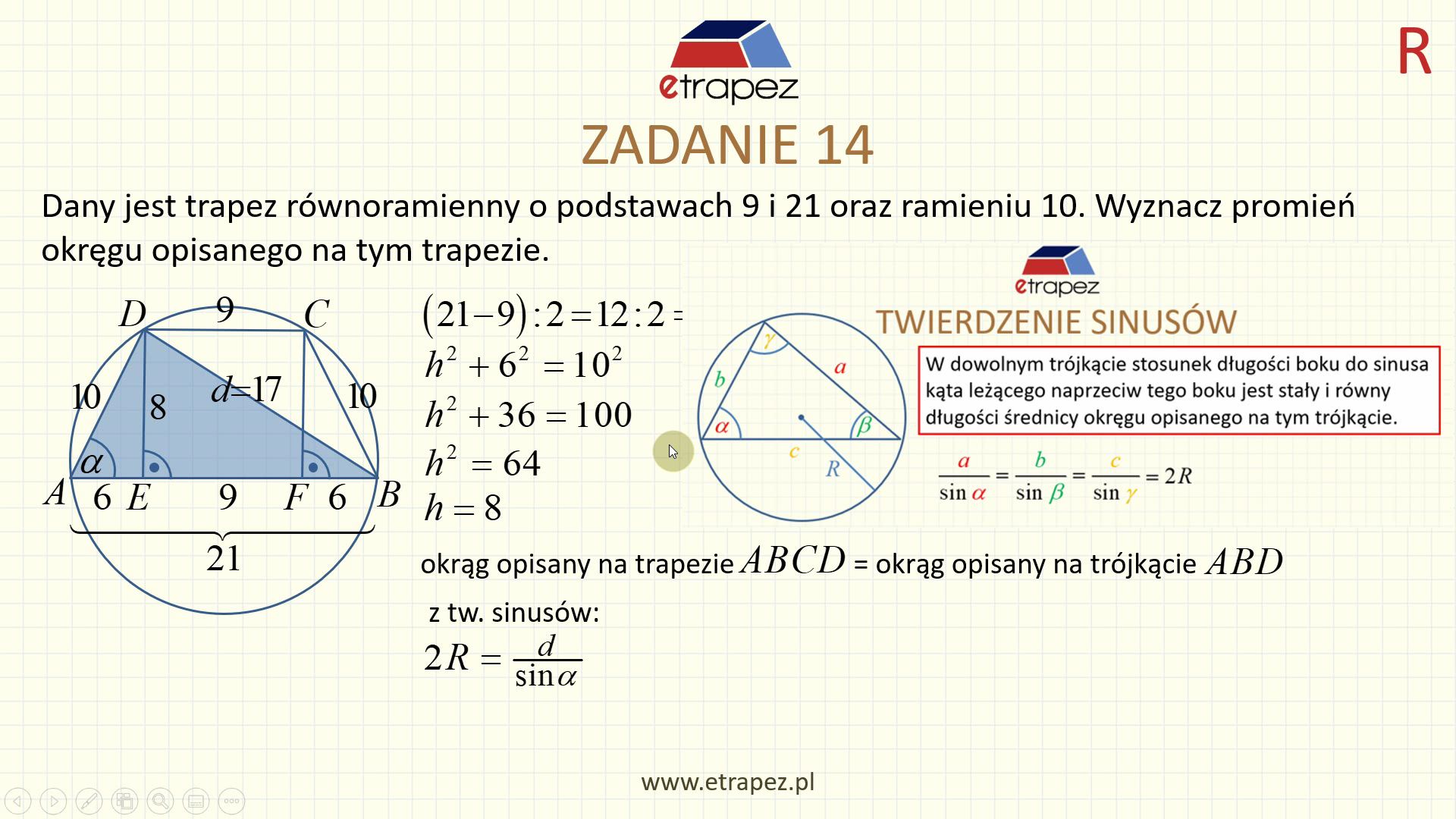
- Zadanie 15: trapez równoramienny, wpisano w niego okrąg o promieniu r, obliczenie promienia okręgu opisanego na trapezie [1:41:27]
- Zadanie 16: dowód – trójkąt równoboczny, dowolny punkt P wewnątrz trójkąta, odległość punku P jest stała [1:53:04]
- Zadanie 17: dowód – suma długości dwóch środkowych w trójkącie jest mniejsza od jego obwodu, nierówność trójkąta [1:58:25]
- Zadanie 18: dowód – wzór na promień okręgu wpisanego w trójkąt prostokątny, twierdzenie o okręgach stycznych [2:03:09]
- Zadanie 19: dowód – trójkąt ostrokątny, poprowadzone dwie wysokości i środkową, zależności między odcinkami [2:08:21]
- Zadanie 20: dowód – trójkąt ostrokątny, poprowadzone dwie wysokości, zależności między wybranymi kątami [2:15:29]
- Zadanie 21: dowód – trójkąt ostrokątny, poprowadzone środkowa i odcinek dzielący środkową na pół, zależności między odcinkami, twierdzenie Talesa, trójkąty podobne [2:19:32]
- Zadanie 22: dowód – trapez, podana skala podobieństwa, zależności między polami trójkątów [2:27:45]
- Zadanie 23: trójkąt prostokątny, okrąg wpisany w trójkąt, długość odcinka łączącego środek przeciwprostokątnej z punktem styczności okręgu z dłuższą przyprostokątną [2:38:41]
- Zadanie 24: trójkąt, podzielony na dwa trójkąty, zastosowanie twierdzenia cosinusów [2:45:08]
- Zadanie 25: trapez prostokątny, okrąg wpisany w trapez, odległości środka okręgu od końców dłuższego ramienia, obliczenie obwodu trapezu [2:51:17]
- Zadanie 26: równoległobok, podany kąt ostry i odległości punktu przecięcia przekątnych od dwóch sąsiednich boków, cosinus kąta przecięcia przekątnych [2:59:11]
- Zadanie 27: trapez równoramienny, przekątne są dwusiecznymi kątów, obliczenie pola koła wpisanego w mniejszy trójkąt CDM [3:11:22]
- Zadanie 28: trójkąt równoramienny o podanych bokach, przedłużono podstawę, narysowano różne odcinki, dołożenie układu współrzędnych, długość odcinka [3:23:29]
- Zadanie 29: kwadrat, podzielony na kilka trójkątów, pole jednego z nich [3:36:35]
- Zadanie 30: trapez, podzielony na trapez, trójkąt i równoległobok [3:46:16]
Ta zawartość dostępna jest po zakupie Kursu