Uwagi
- Równania wpisujemy korzystając Ogólnej instrukcji wpisywania formuł matematycznych
- Równania krzywych oddzielamy przecinkiem
- Liczby dziesiętne wpisujemy z kropką, a nie przecinkiem. Czyli np: 0.1, a nie: 0,1.
- Kalkulator nie jest doskonały. Czasami gubi się przy większej ilości krzywych. Należy zawsze sprawdzić, czy pokazane przez niego pole i całka do policzenia mają sens (patrz Przykład 4).
Przykład 1
Oblicz pole obszaru ograniczonego parabolami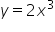 
i 
.
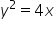Wprowadzam do kalkulatora 'y=2x^3,y^2=4x’:
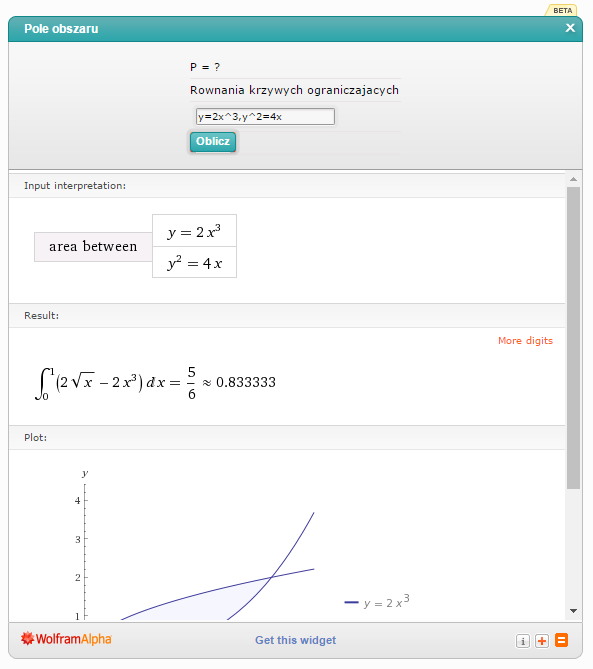
Odp.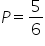 
.
Przykład 2
Oblicz pole obszaru ograniczonego krzywymi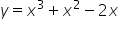 
, osią OX i prostymi 
.
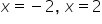Równanie osi OX to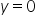 
. Wpisuję do kalkulatora: 'y=x^3+x^2-2x, y=0, x=-2, x=2′:
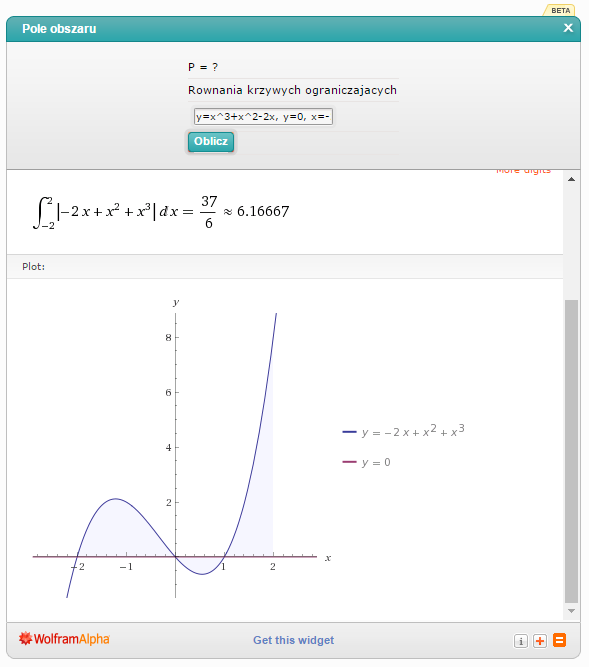
Odp.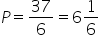 
.
Przykład 3
Oblicz pole obszaru ograniczonego krzywą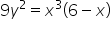 
.
Wpisuję w kalkulator: '9y^2=x^3(6-x)’:
Dostaję komunikat o błędzie:
Przekształcam równanie krzywej:
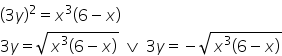
Wpisuję w kalkulator: '3y=sqrt(x^3(6-x)), 3y=-sqrt(x^3(6-x))’.
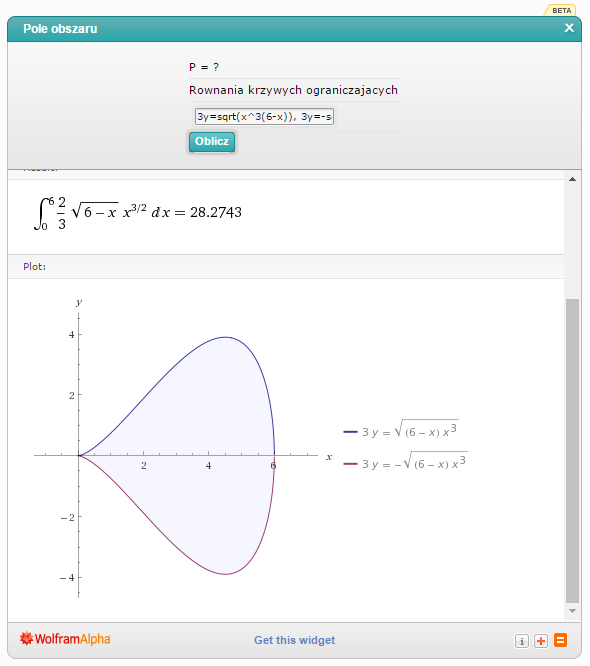
Odp. Pole to wynosi 28,2743 (w przybliżeniu, zapewne).
Przykład 4 (na błędne działanie)
Oblicz pole obszaru ograniczonego parabolami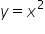 
, 
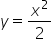i prostą 
.
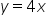Wpisuję w kalkulator 'y=x^2,y=x^2/2,y=4x’:
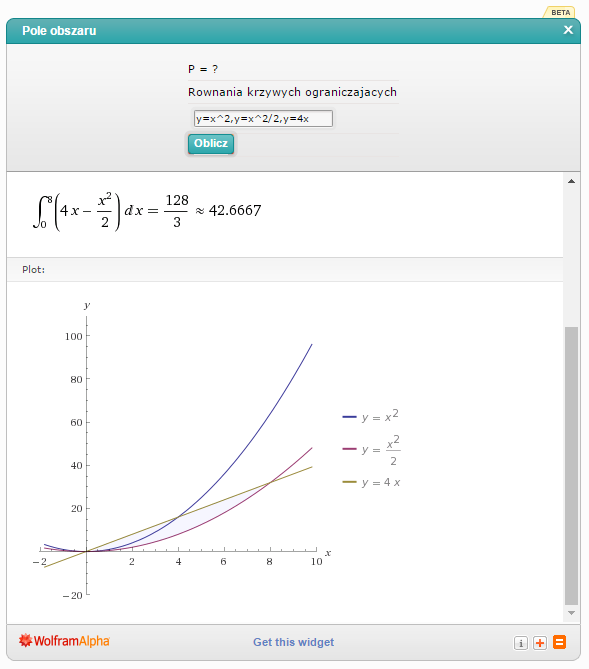
Pozornie wszystko się zgadza, ale widać, że kalkulator źle zaznaczył pole pomiędzy tymi kilkoma krzywymi. Parabola 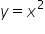w żaden sposób nie bierze udziału w ograniczaniu pola, wręcz mogło by jej nie być. Widać to także w stworzonej przez kalkulator całce oznaczonej.
Wynik nie jest więc prawidłowy.
Możemy podzielić pole na dwa i policzyć osobno.
Pole 1 (pomiędzy parabolą 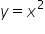, a parabo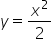lą , dla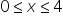 
)
Wpisuję w kalkulator 'y=x^2,y=x^2/2,x=4,x=0′:
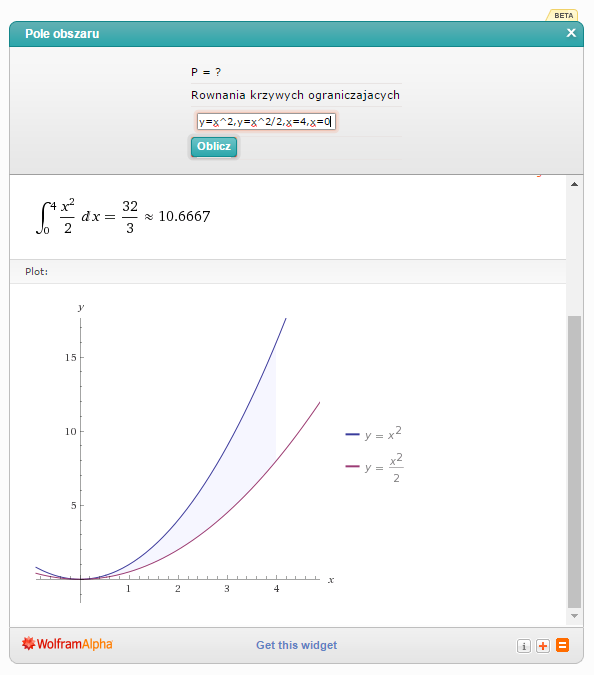
Czyli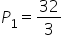 
.
Pole 2 (pomiędzy prostą 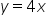, a parabo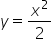lą , dla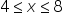 
)
Wpisuję w kalkulator 'y=4x,y=x^2/2,x=4,x=8′:
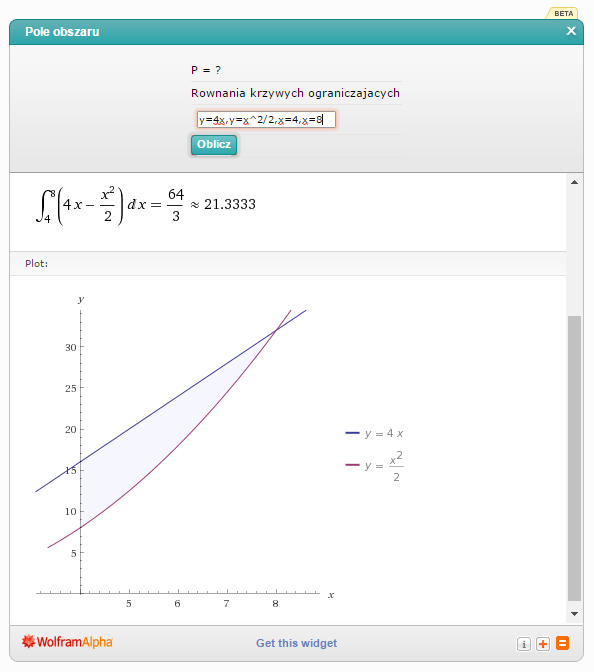
Jak widać, rysunek znowu niezbyt się udał, natomiast sama całka oznaczona (a więc także i wynik) jest prawidłowa.
.
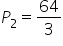Mamy więc wynik.
Odp.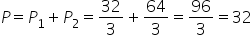 
.
