Uwagi
- Wzór funkcji wpisujemy korzystając Ogólnej instrukcji wpisywania formuł matematycznych
- Liczby dziesiętne wpisujemy z kropką, a nie przecinkiem. Czyli np: 0.1, a nie: 0,1.
Interpretacja wyników
„Horizontal asymptote”
To asymptoty poziome.
Liczba, do której dąży wyrażenie funkcji, to równanie asymptoty.
Na przykład:
„
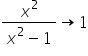as 
„
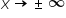Oznacza:
„
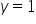jest równaniem asymptoty poziomej przy 
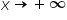i przy 
„
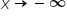„Vertical asymptote”
To asymptoty pionowe.
Liczba, do której dąży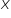 
wyznacza równanie asymptoty.
Na przykład:
„
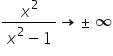as 
„
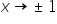Oznacza:
„
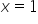i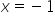 
są równaniami asymptot pionowych”
UWAGA: Kalkulator NIE określa, czy asymptoty są lewo-, prawo- , czy obustronne. Należy to określić samemu na podstawie wykresu.
„Oblique asymptote”
To asymptoty ukośne.
Mamy tu podany wprost wzór na asymptotę ukośną.
Na przykład:
„
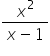is asymptotic to 
„
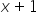Oznacza:
„
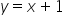jest równaniem asymptoty ukośnej”.
Related Posts
Kalkulator do tautologii
Posted on
