Kalkulator do wykresu i podstawowych własności funkcji (badanie zmienności funkcji)

Uwagi

• Wzór funkcji wpisujemy korzystając Ogólnej instrukcji wpisywania formuł matematycznych
• Liczby dziesiętne wpisujemy z kropką, a nie przecinkiem. Czyli np: 0.1, a nie: 0,1.

Interpretacja wyników

„Plots”

Te dwa wykresy to tak naprawdę jeden i ten sam wykres funkcji, tylko, że w różnych skalach.

Aby uzyskać prawidłowy wykres musisz często zmienić wartość „Complex-valued plot” na „Real-valued plot”.

„Roots”, „Real roots”

To są pierwiastki wykresu, czyli miejsca przecięcia z osią OX, a właściwie ich współrzędne x-sowe (wiadomo, że współrzędne y-kowe równe są 0).

Jeśli uzyskasz „no roots exist”, oznacza to, że funkcja w ogóle nie przecina osi OX

„Domain”

Dziedzina.

„Range”

Zbiór wartości.

„Bijectivity”

„injective” – funkcja jest injekcją (jest różnowartościowa)

„surjective” – funkcja jest surjekcją (jest „typu na”)

„bijective” – funkcja jest bijekcją (jest różnowartościowa i „typu na”)

„Periodicity”

Okresowość funkcji. Np. „periodic with 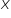 with period 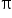” znaczy, że funkcja jest 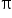-okresowa ( 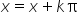dla dowolnego ).

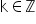„Parity”

„even” – funkcja jest parzysta

„odd” – funkcja jest nieparzysta

„Local/global minimum”

Ekstremum, minimum, lokalne/globalne (przedziałem w globalnym jest dziedzina).

„Local/global maksimum”

Ekstremum, maksimum, lokalne/globalne (przedziałem w globalnym jest dziedzina).