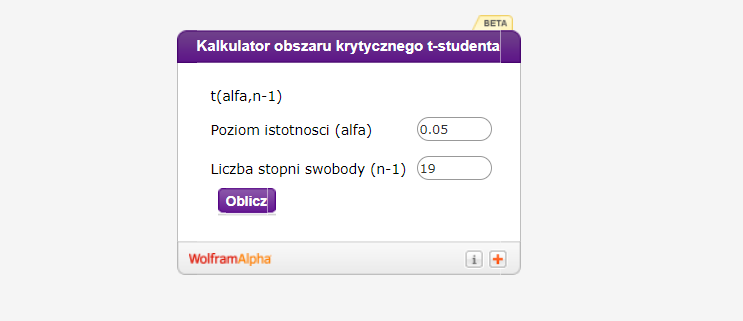
Jeśli potrzeba, kliknij na „Approximate form”, by odczytać przybliżenie wyniku.
Uwagi
- Kalkulator przeznaczony jest do odczytu dwustronnego obszaru krytycznego. Dla obszarów jednostronnych należy wpisać podwojony (dwa razy większy) poziom istotności.
- Liczby dziesiętne wpisujemy z kropką, a nie z przecinkiem. Czyli np: 0.1, a nie 0,1.
Przykład 1 (prosty odczyt z rozkładu)
Odczytaj wartość krytyczną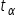 
dla współczynnika ufności 
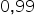i dla liczebności próbki 
.
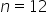Przyjmuję jako poziom istotności (alfa): 0.01, a jako liczbę stopni swobody: 11.
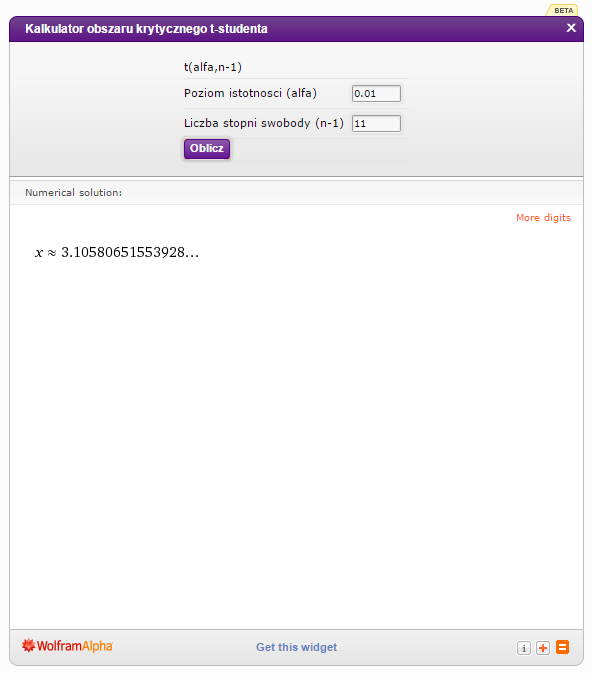
Odp. Wynik to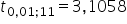 
.
Przykład 2 (przedział ufności)
Oszacować chcemy średnią rozpiętość skrzydełek pewnego gatunku much. W tym celu złapaliśmy 10 much do pudełka i zmierzyliśmy ich rozpiętość skrzydełek. Średnia z tej próbki wyszła nam 0,9 cm, a odchylenie standardowe 2 mm. Przyjmując współczynnik ufności na poziomie 0,9, oszacuj średnią rozpiętość skrzydełek much tego gatunku – zakładając, że rozpiętość ta jest zgodna z rozkładem normalnym.
Skorzystam ze wzoru:
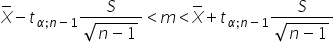
Obliczam do niego tylko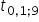 
korzystając z kalkulatora:
Podstawiam wszystko do wzoru i mam:
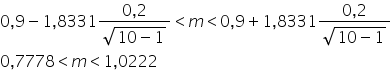
Odp. Na 90% średnia rozpiętości skrzydełek w tej konkretnej muszej populacji mieści się pomiędzy 7,8 milimetra a 1 cm.
Przykład 3 (hipoteza)
Przypuszczamy, że średnia punktów uzyskanych przez studentów za pewne zadanie na kolokwium wynosi 8 pkt. Pewna grupa 26 studentów napisała kolokwium średnio na 10 pkt, z odchyleniem standardowym 4 pkt. Czy nasze przypuszczenie jest słuszne, na poziomie istotności 0.01, przy założeniu, że rozkład punktów uzyskanych przez studentów jest rozkładem normalnym?
Formułuję hipotezy.
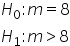
Zwróćmy od razu uwagę, że obszar krytyczny jest jednostronny, będę więc musiał podwoić poziom istotności!
Wpisuję więc do kalkulatora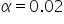 
(podwojenie) i 
:
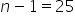Klikam na Approximate form, żeby uzyskać przybliżony wynik:
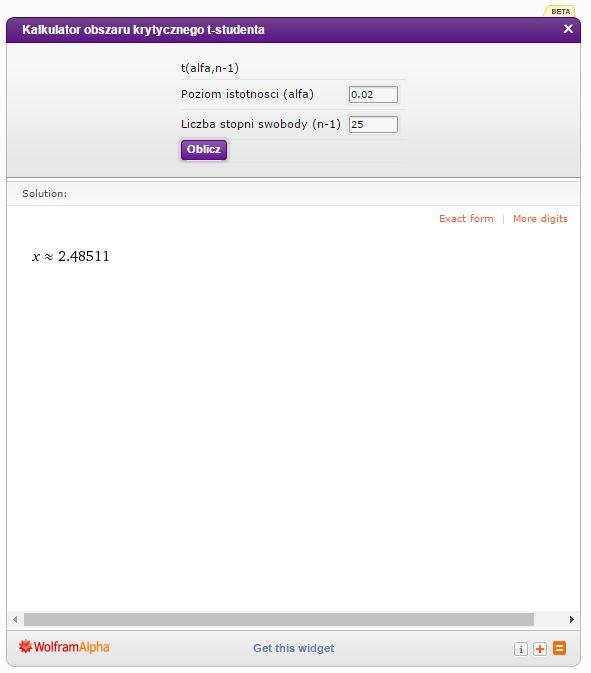
Mam więc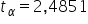 
.
Obliczam teraz wartość 
:
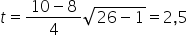
Ponieważ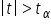 
, należy odrzuć hipotezę 
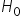na rzecz hipotezy 
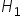. Oznacza to, że na 99% studenci są lepsi w rozwiązywaniu tego zadania, niż przypuszczaliśmy 🙂
