Kalkulator rozkładu Bernoulliego

Przykład 1

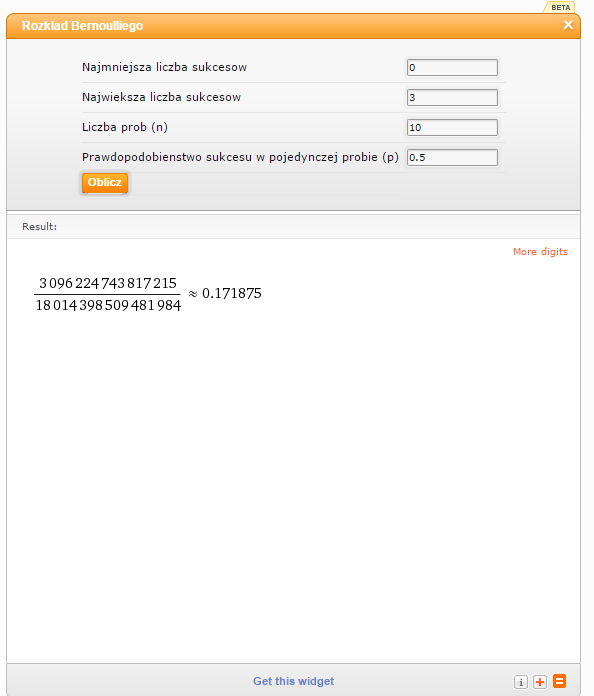
Rzucamy 10 razy monetą. Oblicz prawdopodobieństwo,  że orzeł wypadnie nie więcej niż 3 razy.

Orzeł ma wypaść nie więcej niż 3 razy, czyli ma wypaść 0, 1, 2, albo 3 razy. Jako “Najmniejszą” liczbę sukcesów wpisuję więc 0, a jako “Największą” liczbę sukcesów wpisuję trzy.

Jako liczbę prób wpisuję 10, jako prawdopodobieństwo sukcesu w pojedynczej próbie 0.5 (bo taka jest szansa na wyrzucenie orła w pojedynczym rzucie).

Mam wynik: około 17%.

Przykład 2

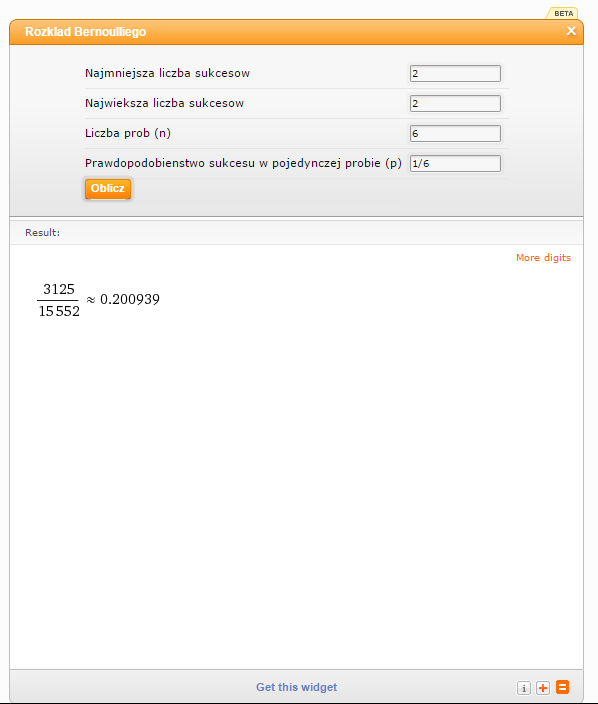
Rzucamy sześcioma kostkami do gry. Jakie są szanse, że sześć oczek wypadnie nam dokładnie na dwóch kostkach?

Ma wypaść dokładnie dwa razy, jako “Najmniejszą” i jako “Największą” liczbę sukcesów wpisuję więc 2. Prób jest 6. Prawdopodobieństwo sukcesu w pojedynczej próbie to 1/6.

Prawdopodobieństwo to wynosi około 0.2

Przykład 3

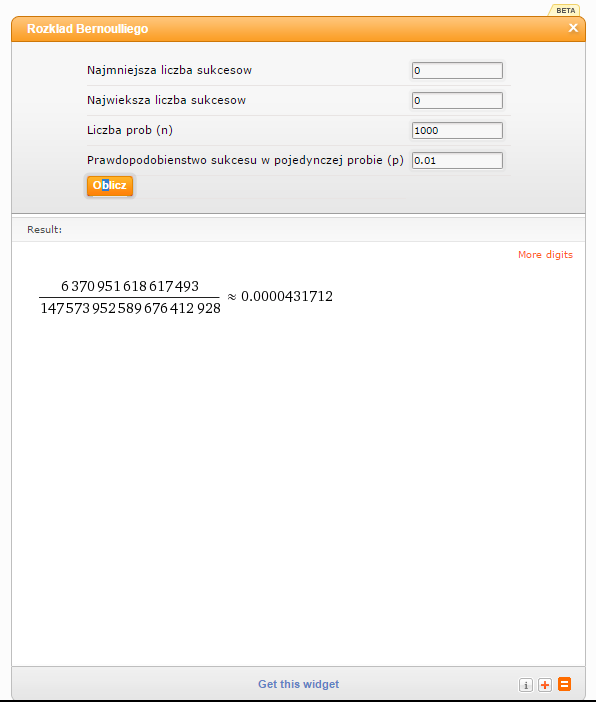
Pewna fabryka produkuje śrubki, z których 1% jest wadliwa. W pudełku znajduje się 1000 śrubek z tej fabryki. Jakie są szanse, że nie ma wśród nich żadnej wadliwej?

Jako “sukces” przyjmuję wadliwość śrubki. Zdarzenie polega więc na tym, że liczba “sukcesów” ma się równać zero, bo w pudełku nie ma być żadnych wadliwych. Przyjmuję “Najmniejszą” i “Największą” liczbę sukcesów jako 0, liczba prób to 1000, prawdopodobieństwo “sukcesu” w pojedynczej próbie to 0,01.

Prawdopodobieństwo zdarzenia jest bardzo małe, wynosi tylko 0,0000431712.

Zwróć uwagę, jak sprawnie kalkulator poradził sobie z gigantyczną liczbą obliczeń w tym przykładzie!