Uwagi
- Ułamki dziesiętne wpisujemy z kropką, a nie z przecinkiem. Czyli 0.1, a nie 0,1.
- W rozkładzie F-Snedecora znaczenie ma kolejność parametrów. Próbki należy odpowiednio ponumerować. Próbka o większej wariancji otrzymuje numer 1, a jej liczebność – 1 to pierwszy parametr. Próbka o mniejszej wariancji otrzymuje numer 2, a jej liczebność -1 to drugi parametr.
- Trzeba uważać na pojęcie „poziom istotności”. Jeśli podamy poziom istotności równy 0.1, kalkulator odczyta nam kwantyl rzędu 0.9.
Przykład 1
Odczytaj wartość rozkładu F-Snedecora dla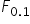 
z parametrami 
.
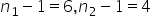Wpisuję bezpośrednio odpowiednie wartości do kalkulatora:
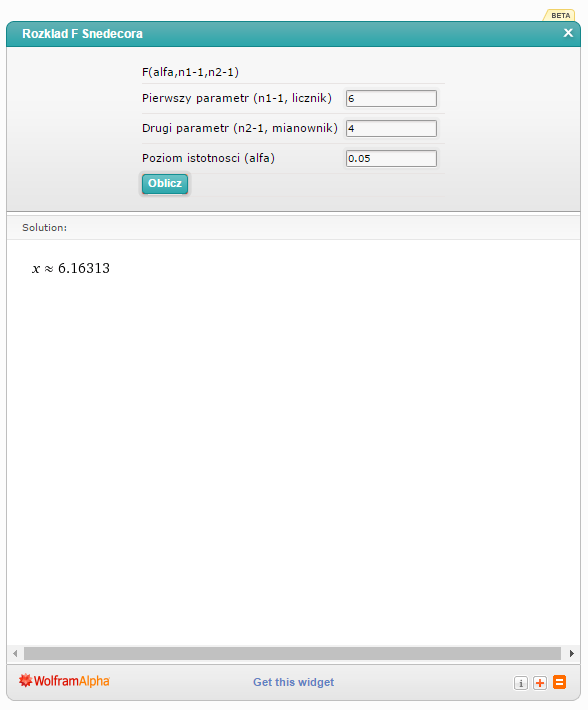
Odp.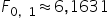 
.
Przykład 2
W celu zmierzenia regularności uzyskiwanych wyników czasowych w biegu na 100 m sprawdzono wyniki zawodników z Europy i Ameryki Południowej. 7 zawodników z Europy uzyskało wariancję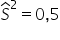 
, 9 zawodników z Ameryki Południowej wariancję równą 
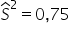. Na poziomie istotności 0,05 zweryfikuj hipotezę, że odchylenia zawodników od średniej z obu kontynentów są takie same. Załóż, że obie populacje mają rozkład normalny.
Wariancja wybranych zawodników z Ameryki Południowej jest większa, oznaczam więc ją jako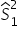 
, a odpowiednio dla całej populacji: 
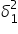. Dla Europy przyjmuję: 
, 
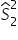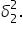
Tworzę hipotezy:
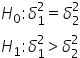
Obliczam wartość odpowiedniej statystyki:
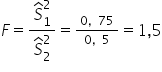
Dalej obliczam wartość krytyczną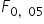 
.
Przyjmuję (patrz uwagi wyżej) za pierwszy parametr 9-1=8. za drugi 7-1=6, za poziom istotności: 0.05.
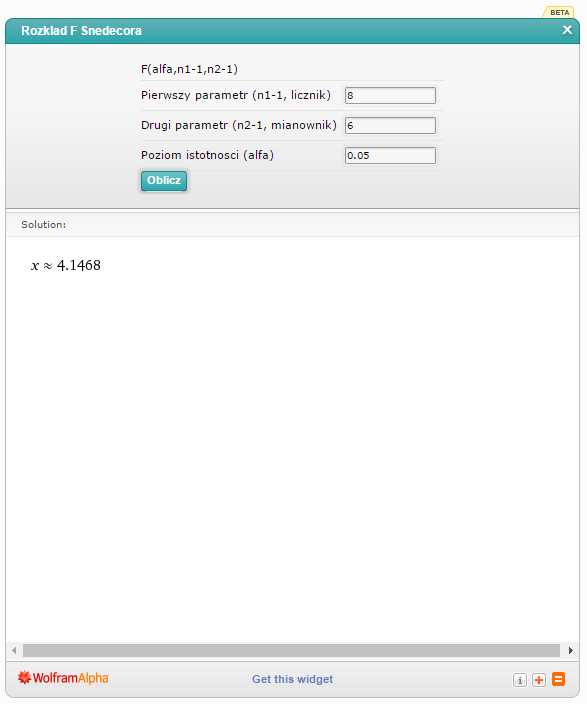
Mam więc: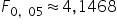 
.
Obszar krytyczny jest prawostronny. Nie jest prawdą, że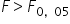 
. Zatem:
Odp. Odchylenia wyników zawodników od średniej są być może takie same na obu kontynentach. Nie mamy podstaw do odrzucenia tej hipotezy na poziomie istotności 0,05.
Related Posts
Kalkulator rozkładu normalnego
Posted on