Kalkulator rozkładu Poissona

Uwagi

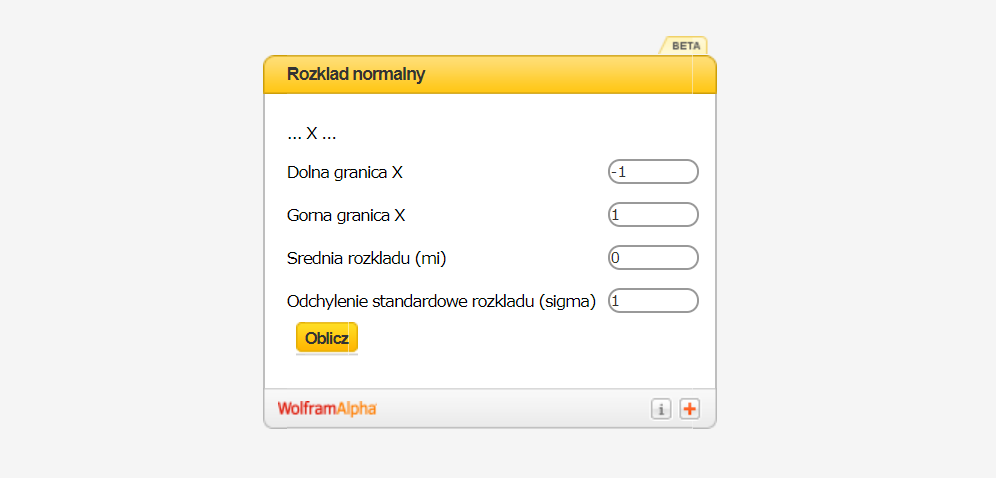
  • ułamki dziesiętne wpisujemy z kropką, a nie z przecinkiem, np. 0.5, a nie 0,5

Przykład 1

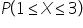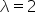Oblicz P open parentheses 1 less or equal than X less or equal than 3 close parentheses w rozkładzie Poissona z parametrem lambda equals 2.

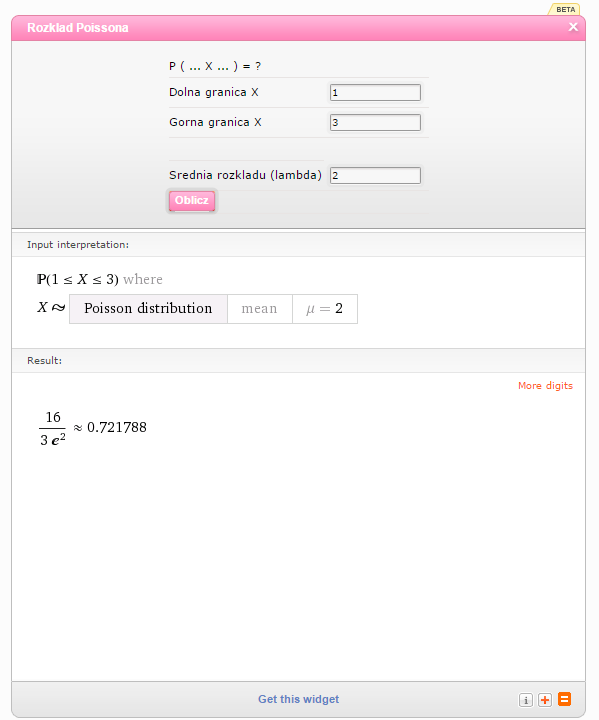
Jako dolną granicę X wpisuję 1, jako górną granicę X wpisuję 3, jako średnią rozkładu wpisuję 2.

Odp. Wynik to 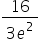fraction numerator 16 over denominator 3 e squared end fraction.

Przykład 2

Prawdopodobieństwo awarii pojedynczego trybiku w złożonym zegarku wynosi 0,001 na 10 lat. W zegarku znajduje się 3000 takich trybików, identycznych i działających niezależnie. Oblicz prawdopodobieństwo, że co najmniej jeden z nich ulegnie awarii w ciągu 10 lat.

Obliczam parametr do rozkładu:

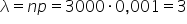
lambda equals n p equals 3000 times 0 comma 001 equals 3

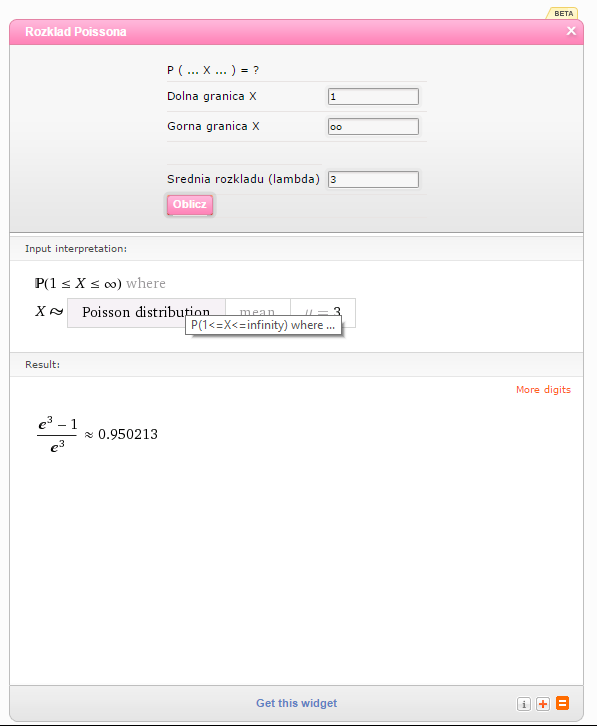
Jako dolną granicę X przyjmuję 1, jako górną ‘oo’, jako średnią 3:

Odp. Prawdopodobieństwo to wynosi około 95%.

Przykład 3

Prawdopodobieństwo trafienia piłką do golfa za pierwszym razem do dołka wynosi 0,003745. Grający na polu golfowym wykonali 4721 identycznych, niezależnych prób. Jaka jest szansa, że nikomu nie udało się trafić do dołka za pierwszym razem?

Obliczam parametr rozkładu, czyli średnią:

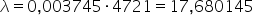
lambda equals 0 comma 003745 times 4721 equals 17 comma 680145

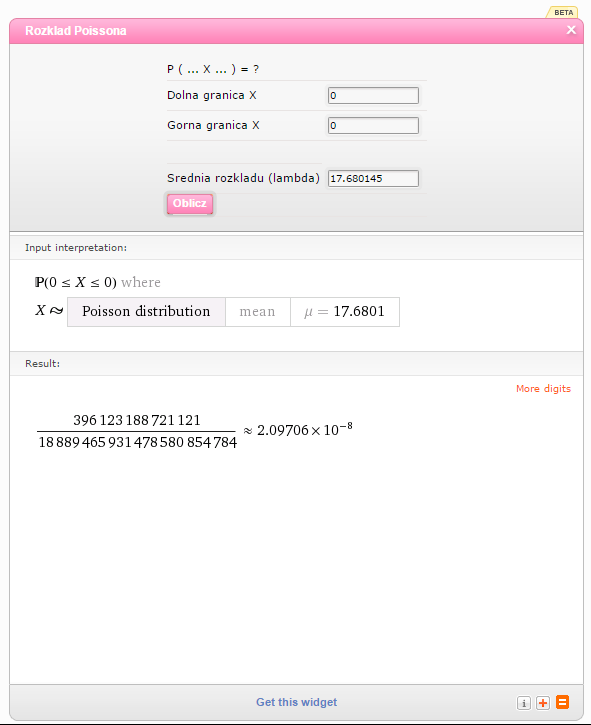
Przyjmuję jako dolną granicę X zero, jako górną zero (otrzymam w ten sposób 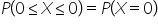P open parentheses 0 less or equal than X less or equal than 0 close parentheses equals P open parentheses X equals 0 close parentheses ), jako średnią rozkładu 17,680145:

Odp. Szansa na zajście tego zdarzenia jest astronomicznie mała i wynosi 0,0000000209706.