Archiwa Studia - Strona 4 z 5

Lekcja 1 – Wprowadzenie do granic ciągów. Wyciąganie przed nawias największej potęgi

Długość: 75 minutyAutor: Krystian KarczyńskiTrudność: Łatwa

Ta Lekcja wprowadza do tematu granic ciągów. Pokazuję od razu na niej pierwszą, podstawową metodę obliczania tych granic - "wyciągania przed nawias".<br /><br /> Dowiesz się z niej, miedzy innymi, jak w prosty sposób zrozumieć, czym są granice ciągów i jak bardzo <strong>przydaje się</strong> to do ich obliczania.<br /><br /> Poznasz również dwa podstawowe, elementarne i <strong>wykorzystywane na każdym kroku </strong>wzory na granice, o istnieniu których wielu nawet nie ma pojęcia, zaczynając naukę.<br /><br /> <h3>Spis treści</h3> <ul> <li>intuicyjne przybliżenie pojęcia granicy ciągu i jej formalna definicja [02:21]</li> <li>ciągi - 5 przykładów [12:17]</li> <li>symbole nieoznaczone [22:48]</li> <li>wyciąganie największej potęgi przed nawias - 20 przykładów [25:45]</li> <li>wyciąganie największej potęgi przed nawias w funkcjach wykładniczych - 3 przykłady [01:00:46]</li> <li>wyciąganie największej potęgi przed nawias w przykładach z silniami - 2 przykłady [01:08:02]</li> </ul>

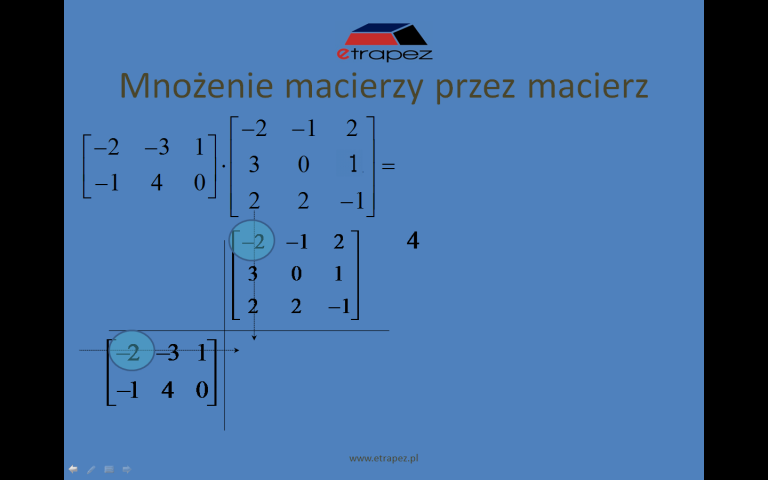
Lekcja 1 – Wprowadzenie do zbiorów. Podstawowe pojęcia.

Długość: 98 minutyAutor: Krystian KarczyńskiTrudność: Łatwa

Wprowadzająca Lekcja do Kursu Zbiory. Zaczynamy zbiorami - co to są zbiory, wyznaczamy pewne zbiory, liczymy ich elementy, sprawdzamy, czy zawierają się w innych...<br /><br /> Na tej Lekcji wprowadzam również pojęcie "języka formalnego" i alfabetów.<br /><br /> Rozwiązałem na niej kilkadziesiąt przykładów (każdy podpunkt liczę jako przykład). Pokazuję i ostrzegam przed różnymi "zmyłkami" w przykładach, takimi jak zbiory będące elementami innych zbiorów, zbiór pusty jako zbiór itp.<br /><br /> <h3>Spis treści</h3> <ul> <li>podstawowe pojęcia związane ze zbiorami: zbiór jako pojęcie pierwotne, element, zapis zbioru, równość zbiorów, zawieranie się zbiorów [7:40]</li> <li>pojęcie zbioru pustego [19:52]</li> <li>pojęcie zbioru potęgowego [24:20]</li> <li>zadanie 1 - wyznacz cztery elementy wskazanych zbiorów (5 przykładów) [29:09]</li> <li>zadanie 2 - wyznacz elementy zbiorów, o ile to możliwe (15 przykładów) [34:45]</li> <li>zadanie 3 - liczenie liczby elementów zbiorów (7 przykładów) [49:20]</li> <li>zadanie 4 - relacje zawierania („inkluzji”) zbiorów (16 przykładów) [55:53]</li> <li>przykład na równość zbiorów i elementów [1:13:13]</li> <li>wprowadzenie do pojęć z języków formalnych: alfabet, litery, słowa, język [1:14:50]</li> <li>4 proste przykłady z języków formalnych [1:17:35]</li> <li>języki formalne - problem [1:24:30]</li> <li>2 przykłady na zliczanie liczby słów w podzbiorach języków [1:28:45]</li> <li>4 przykłady na rozpoznawanie słów i alfabetów [1:32:26]</li> </ul>

Lekcja 1 – Elementy ciągów. Notacja O.

Długość: 97 minutyAutor: Krystian KarczyńskiTrudność: Trudna

Pierwsza część Lekcji poświęcona jest różnym elementom ciągów, sposobom zapisu różnych przydatnych później rzeczy itd.<br /><br /> Na drugiej części zajmuję się notacją O - przydatną w szacowaniu np. efektywności algorytmów.<br /><br /> <h3>Spis treści</h3> <ul> <li>wprowadzenie do pojęcia ciągu [1:52]</li> <li>zadanie 1: ciągi - wyznaczanie wyrazów - 3 przykłady [7:25]</li> <li>zadanie 2: ciągi - wyznaczanie zależności między wyrazami ogólnymi - 2 przykłady [12:08]</li> <li>suma liczb (oznaczenie: wielkie sigma) [15:19]</li> <li>iloczyn liczb (oznaczenie: wielkie pi) [18:04]</li> <li>silnia - wprowadzenie [19:37]</li> <li>ciąg jako funkcja, dziedzina i wartości ciągu [23:11]</li> <li>zadanie 3: ciąg i suma wyrazów [25:35]</li> <li>ciąg zbiorów wraz z przykładami [27:27]</li> <li>suma i iloczyn ciągu zbiorów [30:07]</li> <li>zadanie 4: wyznaczanie sumy i iloczynu ciągu zbiorów [32:24]</li> <li>zagadnienie szybkości wzrostu ciągu - wprowadzenie [35:54]</li> <li>wprowadzenie do notacji O na przykładach [43:50]</li> <li>hierarchia szybkości wzrostu ciągów [58:35]</li> <li>definicja notacji O [1:02:21]</li> <li>własności notacji O [1:04:07]</li> <li>zadanie 5: notacja O wielomianowa - 5 przykładów [1:06:37]</li> <li>zadanie 6: szacowanie ciągów przy pomocy notacji O - 6 przykładów [1:09:35]</li> <li>zadanie 7: sprawdzanie czy podane ciągi dobrze oszacowano przy pomocy notacji O - 9 przykładów [1:14:26]</li> <li>zadanie 8: działania na ciągach z notacją O - 2 przykłady [1:21:32]</li> <li>zadanie 9: wykazywanie, że funkcja wykładnicza jest rzędu co najwyżej n! [1:24:06]</li> <li>zadanie 10: udowadnianie, że suma odwrotności kwadratów jest rzędu co najwyżej 1 [1:29:56]</li> </ul>

Lekcja 1 – Wprowadzenie do logiki

Długość: 73 minutyAutor: Krystian KarczyńskiTrudność: Standardowa

Tą Lekcją rozpoczynam kolejną dużą część Kursu - logikę.<br /><br /> Wprowadzam podstawowe pojęcia - zdania i formy logiczne, a także kwantyfikatory.<br /><br /> <h3>Spis treści</h3> <ul> <li>wprowadzenie do pojęcia zdania logicznego, różnice ze zdaniem w języku polskim [4:04]</li> <li>wprowadzenie do negacji i podstawowych spójników logicznych: koniunkcji, alternatywy, implikacji i równoważności [11:53]</li> <li>zasada kontrapozycji, zdania równoważne [25:47]</li> <li>zdania odwrotne i kontrapozycje - 4 przykłady [28:01]</li> <li>zdania na implikacje - 5 przykładów [31:55]</li> <li>podstawowe spójniki logiczne - równoważność [35:58]</li> <li>formułowanie zdań w symbolice logicznej - zadanie 1 [38:27]</li> <li>formułowanie zdań w symbolice logicznej - zadanie 2 [42:05]</li> <li>wprowadzenie do kwantyfikatorów [45:41]</li> <li>zadanie na kwantyfikatory - 6 przykładów [50:54]</li> <li>zadanie na kwantyfikatory w twierdzeniu [55:57]</li> <li>zadanie na znajdywanie kontrprzykładów do tezy z kwantyfikatorem ogólnym - 6 przykładów [1:01:19]</li> <li>zadanie na wprowadzone na Lekcji pojęcia - 5 przykładów [1:07:54]</li> </ul>

Lekcja 1 – Wprowadzenie do macierzy, podstawowe działania

Długość: 30 minutyAutor: Krystian KarczyńskiTrudność: Łatwa

Z lekcji dowiesz się, jakie jest największe zagrożenie podczas obliczania macierzy i jak sobie z nim poradzić. <p>Pokażę Ci w związku z tym zagrożeniem, jak wygodnie rozpisywać operacje takie jak mnożenie macierzy, <strong>bez konieczności wykonywania wielu operacji w pamięci.</strong></p> <h3>Spis treści</h3> <ul> <li>pojęcie macierzy i podstawowych terminów związanych z macierzą (wiersz, kolumna, wymiar) [04:19]</li> <li>podstawowe operacje na macierzach [06:14]</li> <li>dodawanie macierzy [06:35]</li> <li>odejmowanie macierzy [09:10]</li> <li>kiedy można dodawać i odejmować macierze [11:06]</li> <li>mnożenie macierzy przez liczbę [12:25]</li> <li>mnożenie macierzy przez macierz [13:48]</li> <li>transponowanie macierzy [21:53]</li> <li>podnoszenie macierzy do potęgi [23:17]</li> <li>3 przykłady łączące wszystkie działania [24:25]</li> </ul>

Lekcja 1 – Wprowadzenie do grafów. Podstawowe pojęcia.

Długość: 50 minutyAutor: Krystian KarczyńskiTrudność: Łatwa

Lekcja wprowadzająca do grafów. Sprawdzamy, czym właściwie są grafy i podstawowe związane z nimi pojęcia: droga, cykl, wierzchołki, krawędzie...<br /><br /> Rysujemy wykresy i tworzymy tabelki grafów.<br /><br /> Na początek możesz powtórzyć sobie trochę wprowadzenie do relacji (ale nie jest to koniecznie potrzebne): <ul> <li class="cat-item cat-item-513"><a href="https://online.etrapez.pl/lesson/lekcja-2-wprowadzenie-do-relacji/">Lekcja 2 (Kurs Relacje i Funkcje) – Wprowadzenie do relacji</a></li> </ul> <h3>Spis treści</h3> <ul> <li>przykłady wykresów [3:15]</li> <li>definicje grafu nieskierowanego i skierowanego [5:58]</li> <li>zadanie na rysowanie wykresu grafu o zadanych wierzchołkach i krawędziach [13:34]</li> <li>zadanie na tworzenie tabelki do grafu o danym wykresie [19:17]</li> <li>definicja drogi i długości drogi [22:50]</li> <li>zadanie na drogi i ich zapis przy pomocy wierzchołków [23:44]</li> <li>definicja cyklu, drogi acyklicznej i grafu acyklicznego [27:25]</li> <li>zadanie na szukanie cyklów i określanie acykliczności [29:09]</li> <li>zadanie na rysowanie grafu z danych tekstowych [38:20]</li> <li>definicje wierzchołków sąsiednich, osiągalności, pętli, krawędzi wielokrotnych [41:22]</li> <li>zadanie na odnajdywanie podstawowych elementów grafu w grafie nieskierowanym [43:55]</li> </ul>

Lesson Tag: Studia

Zaloguj się

Zarejestruj się