Ta Lekcja poświęcona jest różnym typom równań różniczkowym, które można, najczęściej za pomocą jakiegoś podstawienia, sprowadzić do równania o zmiennych rozdzielonych.
Pokazuję też, na co trzeba bardzo uważać przy podstawieniach sprowadzających do równania o zmiennych rozdzielonych.
Spis treści
- typy równań sprowadzalnych do zmiennych rozdzielonych [02:07]
- równania typu y’=f(ax+by+c) – podstawienie i sposób postępowania [05:35]
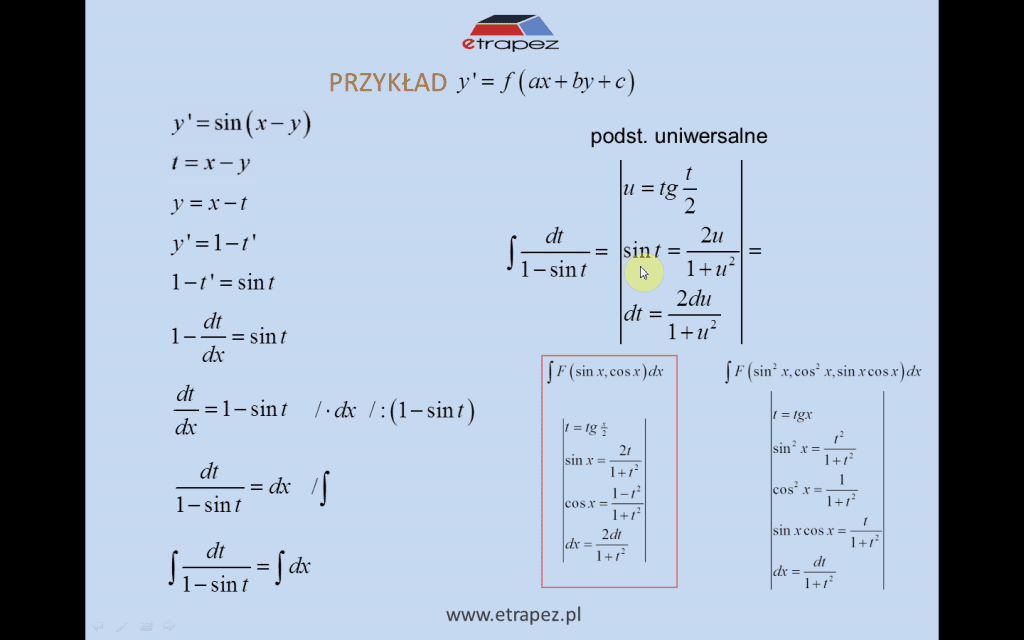
- rozwiązywanie równań typu y’=f(ax+by+c) – przykład 1 [10:09]
- rozwiązywanie równań typu y’=f(ax+by+c) – przykład 2 [18:19]
- rozwiązywanie równań typu y’=f(ax+by+c) – przykład 3 [25:29]
- rozwiązywanie równań typu y’=f(ax+by+c) – przykład 4 [32:52]
- równania typu y’=f(y/x) (jednorodne względem y i x) – podstawienie i sposób postępowania [40:44]
- rozwiązywanie równań typu y’=f(y/x) – przykład 1 [44:07]
- rozwiązywanie równań typu y’=f(y/x) – przykład 2 [47:14]
- rozwiązywanie równań typu y’=f(y/x) – przykład 3 [54:48]
- sprowadzenie równania do równania typu y’=f(y/x) – 4 różne sposoby [01:00:44]
- równania 3-go typu sprowadzalne do zmiennych rozdzielonych – omówienie dwóch przypadków [01:05:46]
- trzeci typ równań sprowadzalnych do zmiennych rozdzielonych – przykład 1 [01:10:23]
- trzeci typ równań sprowadzalnych do zmiennych rozdzielonych – przykład 2 [01:16:58]
