Na tej Lekcji przerabiam zbiory częściowo uporządkowane wraz z pojęciami z nimi związanymi: diagramami Hassego, elementami maksymalnymi/minimalnymi/najmniejszymi/największymi, kresami. Przed rozpoczęciem musisz już mieć opanowane:
Relacje częściowego porządku to relacje, które są:
- zwrotne
- antysymetryczne
- przechodnie
Relacje częściowego porządku „porządkują” zbiory, wyznaczając elementy „większe” i „mniejsze”. Lekcja trwa około godzinę i 45 minut.
Spis treści:
- definicja relacji częściowego porządku [2:24]
- 4 przykłady relacji częściowego porządku [5:50]
- umowne słownictwo i oznaczenia używane w relacjach częściowego porządku [10:03]
- zadanie 1: sprawdzenie, czy relacja jest relacją częściowego porządku – 4 przykłady [11:46]
- wprowadzenie do diagramów Hassego [16:07]
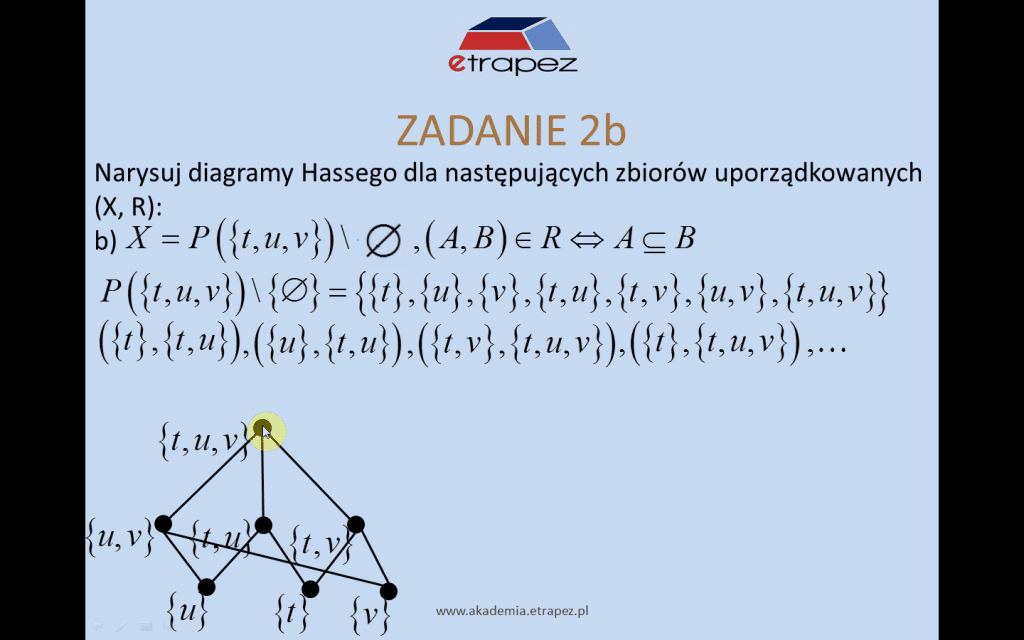
- zadanie 2: rysowanie diagramów Hassego – 3 przykłady [18:15]
- definicja elementów maksymalnych i minimalnych [34:46]
- 3 przykłady na odczytywanie elementów maksymalnych i minimalnych z diagramu Hassego [37:09]
- definicja elementów największych i najmniejszych [44:00]
- 3 przykłady na odczytywanie elementów największych i najmniejszych z diagramu Hassego [46:07]
- różnice pomiędzy elementami maksymalnymi/minimalnymi, a największymi/najmniejszymi [49:10]
- zadanie 3: sprawdzanie czy relacja jest relacją częściowego porządku [50:09]
- zadanie 4: sprawdzanie czy relacja jest relacją częściowego porządku, wyznaczenie elementów wyróżnionych (np. maksymalne) [52:50]
- definicja kresów (supremum i infimum) [58:51]
- 3 przykłady na kresy [1:01:22]
- definicja kraty wraz z przykładem [1:12:07]
- zadanie 5: kraty, elementy wyróżnione, kresy – liczby rzeczywiste z relacją mniejsze lub równe [1:15:29]
- zadanie 6: zbiór będący kratą – elementy wyróżnione, diagram Hassego [1:20:00]
- zadanie 7: kraty, elementy wyróżnione, diagram Hassego – zbiór wraz z relacją podzielności [1:30:10]
- zadanie 8: kraty, elementy wyróżnione – nieparzyste podzbiory liczb naturalnych [1:35:36]
- zadanie na dowodzenie [1:40:03]
Zadanie Domowe
Pobierz Rozwiązania Zadania Domowego (PDF)
Dodatkowe materiały video
Ten filmik należy traktować jako materiał uzupełniający do właściwej Lekcji 5, nakręciłem go kilka lat temu, nie myśląc o dodaniu do Kursu Matematyki Dyskretnej.
Pokazuję na nim bliżej kresy zbiorów liczbowych z relacją zwykłego porządku między liczbami – i tylko takie!!!
Video ma prawie 45 minut.
Spis treści:
- przykłady zbiorów liczbowych o różnym zapisie [0:39]
- elementy kresów zbioru [4:40]
- definicja ograniczenie zbioru (z dołu lub z góry) [5:30]
- definicja najmniejszej i największej wartości w zbiorze (min i max) [8:05]
- definicja kresu dolnego i górnego zbioru (inf i sup) [10:28]
- przykład 1: kresy zbioru – ułamki a/b [14:24]
- przykład 2: kresy zbioru nieskończonego [22:44]
- przykład 3: kresy zbioru k/(k+1) [25:55]
- przykład 4: kresy funkcji x/(x^2+1) [28:27]
- przykład 5: kresy zbiorów An, graniczoność i kresy uogólnionej nieskończonej sumy An [37:53]