Uwagi
- Liczby dziesiętne wpisujemy z kropką. Czyli 0.1, a nie 0,1.
Przykład 1
Chcemy odczytać 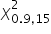 .
.

Klikamy na „Approximate form” i mamy wynik:

Odp. 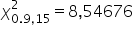 .
.
Przykład 2 (przedział ufności)
Oszacuj wariancję w populacji o rozkładzie normalnym, jeśli wariancja w 21 elementowej próbce wyniosła 44, na poziomie ufności 0,95.
Wzór na odpowiedni przedział ufności to:
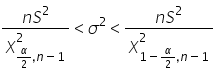
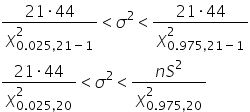
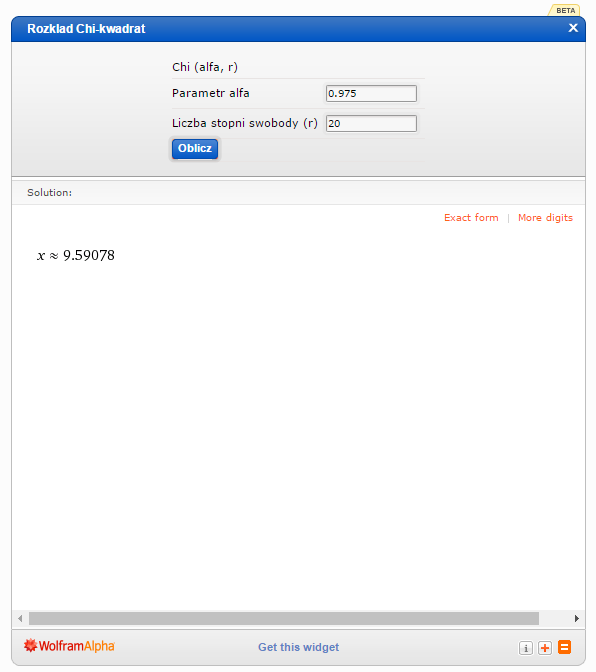
Wartości 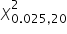 i
i 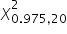 odczytuję z kalkulatora:
odczytuję z kalkulatora:

Podstawiam obliczone wartości do wzoru i mam:
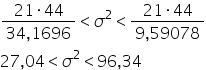
Odp. Na 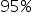 wariancja w populacji mieści się pomiędzy
wariancja w populacji mieści się pomiędzy 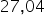 , a
, a 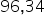 .
.
Przykład 3 (hipoteza)
Losowa próba 37 gospodyń domowych dała wariancję 0,5 kg miesięcznie zużywanego proszku do prania wiodącej na rynku marki. Zakładając, że rozkład zużywanego miesięcznie proszku do prania przez całą populację gospodyń domowych jest rozkładem normalnym, zweryfikuj hipotezę, że odchylenie standardowe w niej wynosi 0,9 kg. Przyjmij poziom istotności 0,05.
Formułuję hipotezy zerową i alternatywną (trzeba przeliczyć odchylenie standardowe na wariancję):
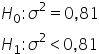
Obliczamy wartość odpowiedniej statystyki:
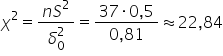
Mam do czynienia tutaj (uwaga!) z lewostronnym obszarem krytycznym. Muszę odczytać więc z tablic rozkładu wartość dla parametru 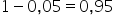 , dla 26 stopni swobody (liczebność próbki minus 1) ,czyli
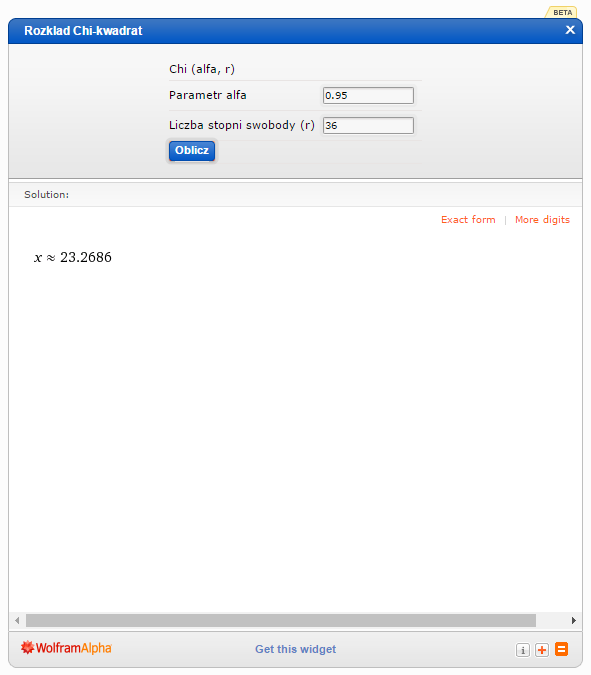
, dla 26 stopni swobody (liczebność próbki minus 1) ,czyli 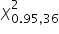 . Robię to przy pomocy kalkulatora:
. Robię to przy pomocy kalkulatora:
Obszar krytyczny jest lewostronny, zatem statystyka 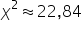 znalazła się w obszarze krytycznym, bo
znalazła się w obszarze krytycznym, bo 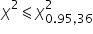 . Zatem na
. Zatem na 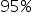 możemy odrzucić hipotezę, że odchylenie standardowe ilości zużytego miesięcznie proszku w tej populacji jest równe 0,9 na rzecz hipotezy, że jest mniejsze.
możemy odrzucić hipotezę, że odchylenie standardowe ilości zużytego miesięcznie proszku w tej populacji jest równe 0,9 na rzecz hipotezy, że jest mniejsze.