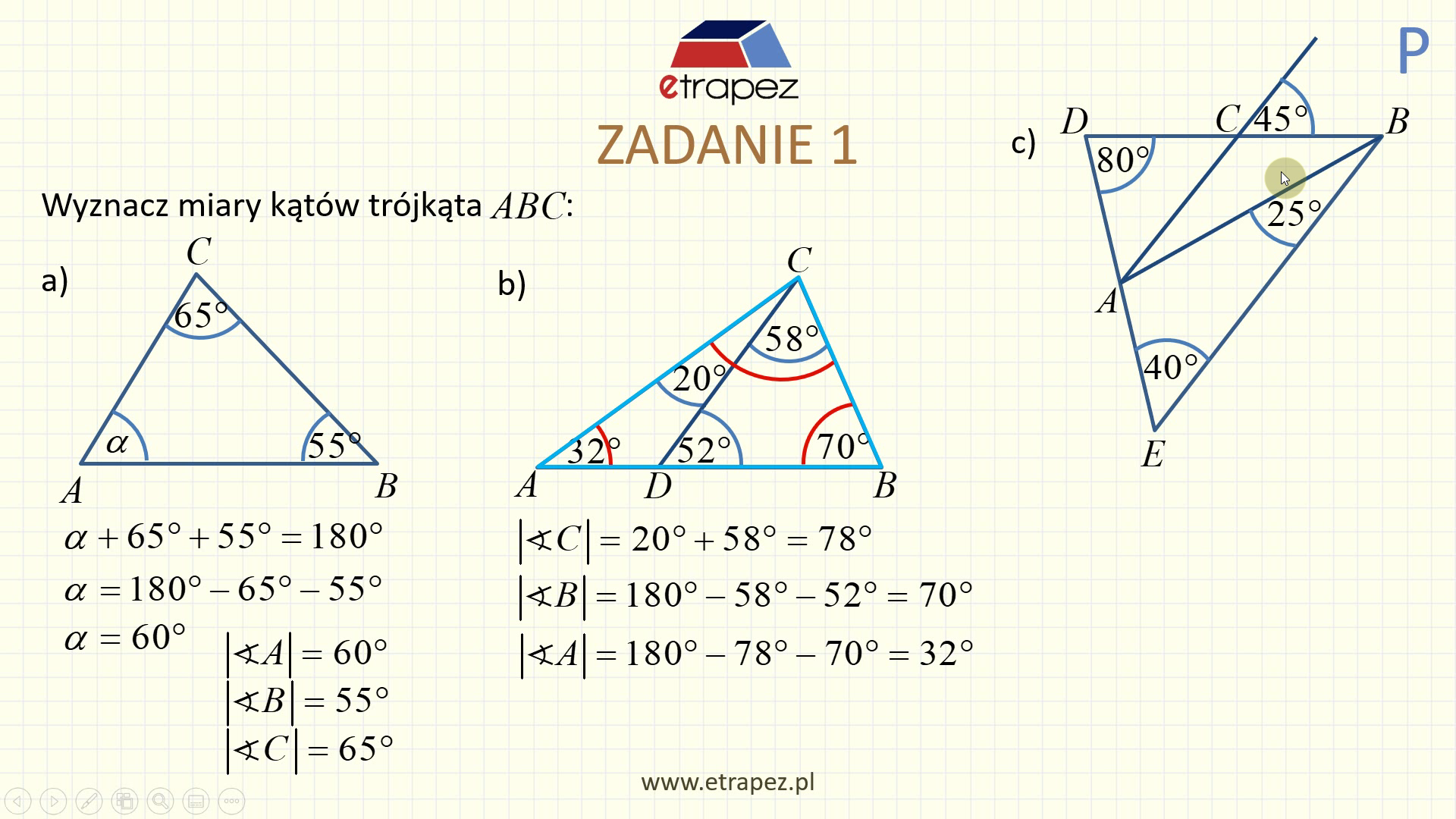
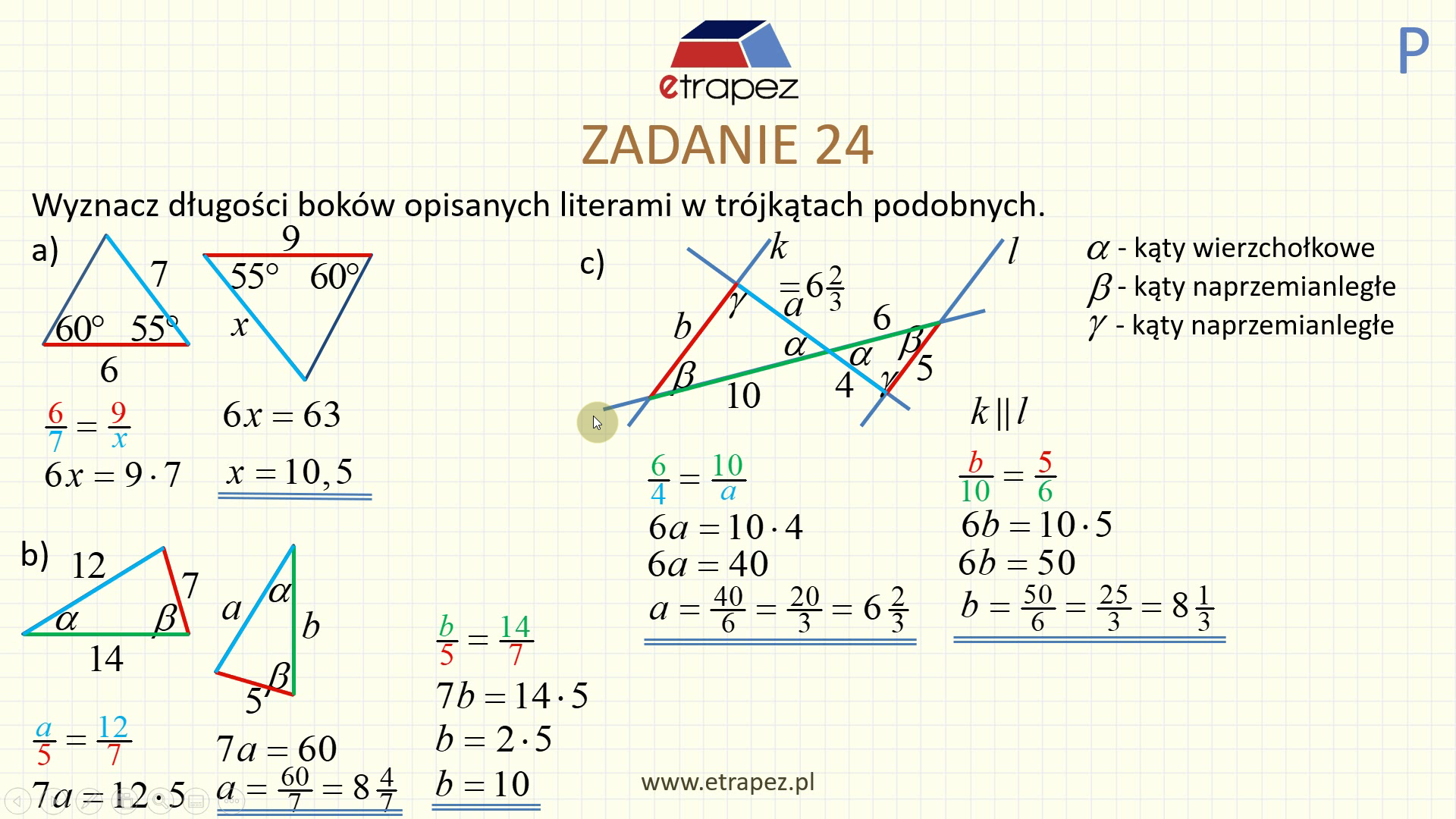
Lekcja 2.4P – Trójkąty – Twierdzenie sinusów i twierdzenie cosinusów

Lekcja druga podstawowa jest podzielona na 5 odrębnych części. Część czwarta poświęcona jest szczególnemu tematowi - twierdzeniu sinusów i cosinusów. Temat ten wcześniej obowiązywał uczniów z poziomu rozszerzonego. Według nowej podstawy programowej, obowiązującej od matury w 2023 roku, temat ten przeszedł na poziom podstawowy. Na blisko 2-godzinnej lekcji omawiam na 13 przykładach sposób stosowania tych twierdzeń w trójkątach. <br/><br/> <h3>Spis treści:</h3> <ul> <li>Twierdzenie sinusów [01:31]</li> <li>Dowód twierdzenia sinusów (3 przypadki) [04:18]</li> <li>Zadanie 33 (a): zastosowanie twierdzenia sinusów w zadaniach [22:26]</li> <li>Zadanie 33 (b): zastosowanie twierdzenia sinusów w zadaniach [25:31]</li> <li>Zadanie 33 (c): zastosowanie twierdzenia sinusów w zadaniach [28:50]</li> <li>Zadanie 33 (d): zastosowanie twierdzenia sinusów w zadaniach [34:18]</li> <li>Zadanie 33 (e): zastosowanie twierdzenia sinusów w zadaniach [37:05]</li> <li>Zadanie 33 (f): zastosowanie twierdzenia sinusów w zadaniach [43:16]</li> <li>Twierdzenie cosinusów [53:02]</li> <li>Twierdzenie cosinusów a twierdzenie Pitagorasa [54:22]</li> <li>Dowód twierdzenia cosinusów (3 przypadki) [57:07]</li> <li>Wnioski z twierdzenia cosinusów [1:12:03]</li> <li>Zadanie 34: zastosowanie twierdzenia cosinusów w zadaniach – 3 przykłady [1:14:14]</li> <li>Zastosowanie twierdzenia cosinusów do określania kątów w trójkącie (dowód) [1:24:27]</li> <li>Zadanie 35: zastosowanie twierdzenia sinusów i cosinusów w zadaniach – 4 przykłady [1:31:11]</li> </ul>